자료구조) AVL 트리

2025-03-07

AVL 트리는 균형이 잡힌 이진 탐색 트리(Balanced Binary Search Tree, BST)이다.

이진 탐색 트리는 데이터 삽입/삭제가 반복되면 한쪽으로 치우칠 수 있어, 탐색 성능이 O(n)까지 저하될 수 있다.

AVL 트리는 이를 방지하고 항상 O(log n) 성능을 유지한다.

AVL 트리가 필요한 이유

이진 탐색 트리(BST)의 한계

이진 탐색 트리는 평균적으로 탐색, 삽입, 삭제가 O(log n) 이지만,

트리가 한쪽으로 기울어진다면 O(n)까지 성능이 저하될 수 있다.

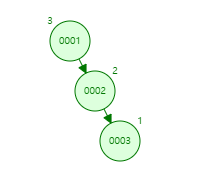
이렇게 한쪽으로 치우치면, 탐색/삽입/삭제 연산이 리스트와 동일한 O(n)이 된다. 즉, BST는 균형을 유지하지 않으면 성능이 저하될 수 있다.

AVL 트리의 해결책

AVL 트리는 모든 노드의 왼쪽, 오른쪽 서브트리의 높이 차이를 항상 1 이하로 유지한다.

이렇게 하면 탐색/삽입/삭제 연산이 항상 O(log n) 을 보장할 수 있다.

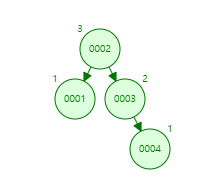
이진 탐색 트리와 동일한 구조를 가지면서도 균형을 유지하여 탐색 성능을 보장한다.

AVL 트리의 균형 유지 기법

AVL 트리는 삽입과 삭제 시 균형(Balance Factor)을 확인하여 회전(Rotation)을 수행한다.

균형 인수 (Balance Factor)

각 노드의 균형 인수(Balance Factor)는 왼쪽 서브트리 높이 - 오른쪽 서브트리 높이로 정의된다.

int Balance(Node* node)
{
    if (node)
        return Base::Height(node->left) - Base::Height(node->right);
    else
        return 0;
}

균형 인수 = 1, 0, -1 → 균형 유지 (No Rotation 필요 없음)
균형 인수 < -1 또는 > 1 → 회전(Rotation) 필요

회전 (Rotation)

트리의 균형이 무너질 경우, 4가지 경우에 따라 회전(Rotation)을 수행한다.

LL (Left-Left) → 오른쪽 회전 (Right Rotation)

균형 인수 > 1, 왼쪽 자식의 균형 인수 >= 0

Node* RotateRight(Node* parent)
{
    Node* child = parent->left;
    parent->left = child->right;
    child->right = parent;
    return child;
}

LL 회전은 왼쪽으로 치우친 경우 해결하는 방법이다.

RR (Right-Right) → 왼쪽 회전 (Left Rotation)

균형 인수 < -1, 오른쪽 자식의 균형 인수 <= 0

Node* RotateLeft(Node* parent)
{
    Node* child = parent->right;
    parent->right = child->left;
    child->left = parent;
    return child;
}

RR 회전은 오른쪽으로 치우친 경우 해결하는 방법이다.

LR (Left-Right) → 좌회전 후 우회전

균형 인수 > 1, 왼쪽 자식의 균형 인수 < 0

if (balance > 1 && Balance(node->left) < 0)
{
    node->left = RotateLeft(node->left);
    return RotateRight(node);
}

RL (Right-Left) → 우회전 후 좌회전

균형 인수 < -1, 오른쪽 자식의 균형 인수 > 0

if (balance < -1 && Balance(node->right) > 0)
{
    node->right = RotateRight(node->right);
    return RotateLeft(node);
}

AVL 트리의 주요 연산

삽입 (Insert)

AVL 트리에서 삽입 후 균형을 확인하고, 필요하면 회전을 수행한다.

Node* Insert(Node* node, const Item& item)
{
    if (!node)
        return new Node{ item, nullptr, nullptr };

    if (item.key < node->item.key)
        node->left = Insert(node->left, item);
    else if (item.key > node->item.key)
        node->right = Insert(node->right, item);
    else
        return node;

    int balance = Balance(node);

    if (balance > 1 && Balance(node->left) >= 0)
        return RotateRight(node);

    if (balance < -1 && Balance(node->right) <= 0)
        return RotateLeft(node);

    if (balance > 1 && Balance(node->left) < 0)
    {
        node->left = RotateLeft(node->left);
        return RotateRight(node);
    }

    if (balance < -1 && Balance(node->right) > 0)
    {
        node->right = RotateRight(node->right);
        return RotateLeft(node);
    }

    return node;
}

시간 복잡도: O(log n)

삭제 (Remove)

AVL 트리는 삭제 후에도 균형을 유지해야 한다.

Node* Remove(Node* node, const K& key)
{
    if (!node) return node;

    if (key < node->item.key)
        node->left = Remove(node->left, key);
    else if (key > node->item.key)
        node->right = Remove(node->right, key);
    else
    {
        if (!node->left)
        {
            Node* temp = node->right;
            delete node;
            return temp;
        }
        else if (!node->right)
        {
            Node* temp = node->left;
            delete node;
            return temp;
        }

        Node* temp = MinKeyNode(node->right);
        node->item = temp->item;
        node->right = Remove(node->right, temp->item.key);
    }

    int balance = Balance(node);

    if (balance > 1 && Balance(node->left) >= 0)
        return RotateRight(node);

    if (balance < -1 && Balance(node->right) <= 0)
        return RotateLeft(node);

    if (balance > 1 && Balance(node->left) < 0)
    {
        node->left = RotateLeft(node->left);
        return RotateRight(node);
    }

    if (balance < -1 && Balance(node->right) > 0)
    {
        node->right = RotateRight(node->right);
        return RotateLeft(node);
    }

    return node;
}

시간 복잡도: O(log n)

AVL 트리 vs. 이진 탐색 트리(BST)

비교 항목	AVL 트리	이진 탐색 트리 (BST)
탐색 속도	O(log n)	평균 O(log n), 최악 O(n)
삽입/삭제 속도	O(log n) (회전 포함)	O(log n), 최악 O(n)
트리 균형 유지	항상 유지	불균형 가능
메모리 사용량	약간 증가 (높이 계산 필요)	적음

결론

AVL 트리는 탐색/삽입/삭제 속도를 O(log n)으로 보장하여, 균형이 유지되는 트리를 제공한다.
일반 BST보다 메모리를 조금 더 사용하지만, 성능 보장을 위해 유용하다.
검색이 많은 경우 AVL 트리를 고려하고, 삽입/삭제가 많으면 Red-Black 트리를 고려할 수 있다.

참고자료

https://www.cs.usfca.edu/~galles/visualization/AVLtree.html

https://www.geeksforgeeks.org/introduction-to-avl-tree/#

Sanghun Lee