Sanghun Lee

Animation Rigger

적응형 걷기 시스템 만들기

캐릭터의 발이 지형에 정확하게 안착하고 자연스럽게 움직이에 만드는 것을 동적으로 만들어 보고 싶었다.

오늘은 Porcedural Animation(절차적 애니메이션)의 개념을 짚어보고, 언리얼 엔진의 Control Rig를 활용해 지형에 반응하는 걷기 애니메이션을 구현해 보고자 한다.

Procedural Animation이란?

먼저 개념을 짚어가자.

우리 말로는 절차적생성 애니메이션이라고 한다.

애니메이터가 수동으로 키프레임 작업하는 대신, 코드와 알고리듬을 사용해 실시간으로 동작을 생성하는 방식을 뜻한다.

왜 중요한가?

실시간 상호작용

흐르는 천, 지형에 맞춰 움직이는 캐릭터의 발, 물리 효과 등 복잡한 환경에 즉각적으로 반응한다.

시간 절약

움직임의 규칙만 정의 된다면, 무한한 변형이 가능하므로 수정 비용이 많이 줄어든다.

다양성

게임 플레이나 물리 법칙에 따라 매번 조금씩 다른, 사실적이로 역동적인 움직임을 만들어낸다.

작동원리

규칙 기반(Rule Base)

프레임 단위 작업이 아닌, 애니메이션을 제어하는 규칙과 변수를 설정한다.

동적 적응(Dynamic Adaptation)

계단의 높이가 달라져도 미리 만든 애니메이션을 교체하는 것이 아니라, 시스템이 다리 높이와 보폭을 계산해 적응한다.

역운동학(Inverse Kinematics)

손이나 발이 목표 지점으로 이동 할 때, 나머지 관절이 자연스럽게 따라오도록 계산한다.

제작 과정

지형 적응형 발 IK 구현하기

이제 실제 Control Rig 노드를 통해 걷기 애니메이션의 핵심인 적응형 다리를 구현해보자.

1. Initialize Bone (Construction Event)

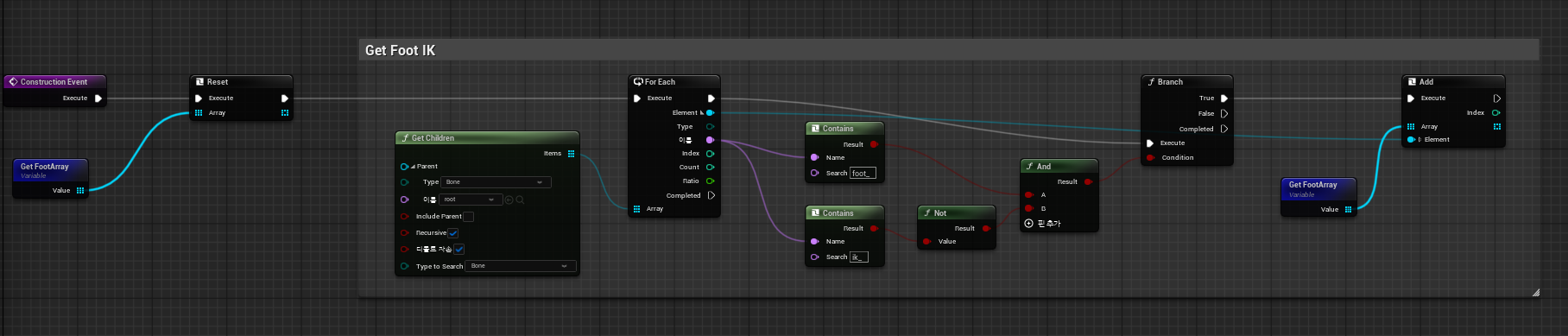
가장 먼저 해야 할 일은 우리가 제어할 발 뼈들을 찾는 것이다.

하드 코딩을 피하기 위해 이름을 기반으로 발 관련 본들을 배열에 담는다.

  • Construction Event : 런타임 이전에 리그가 초기화될 때 실행된다.
  • Get Children을 통해 계층 구조를 돌며, 이름에 foot이 포함되고 ik는 포함되지 않는 본들을 찾아 FootArray에 저장한다. 이렇게 하면 모델이 바뀌어도 본구조가 동일하다면 동일하게 사용 가능하다.

image-20260116224947583

2. 지형 감지(Sphere Trace)

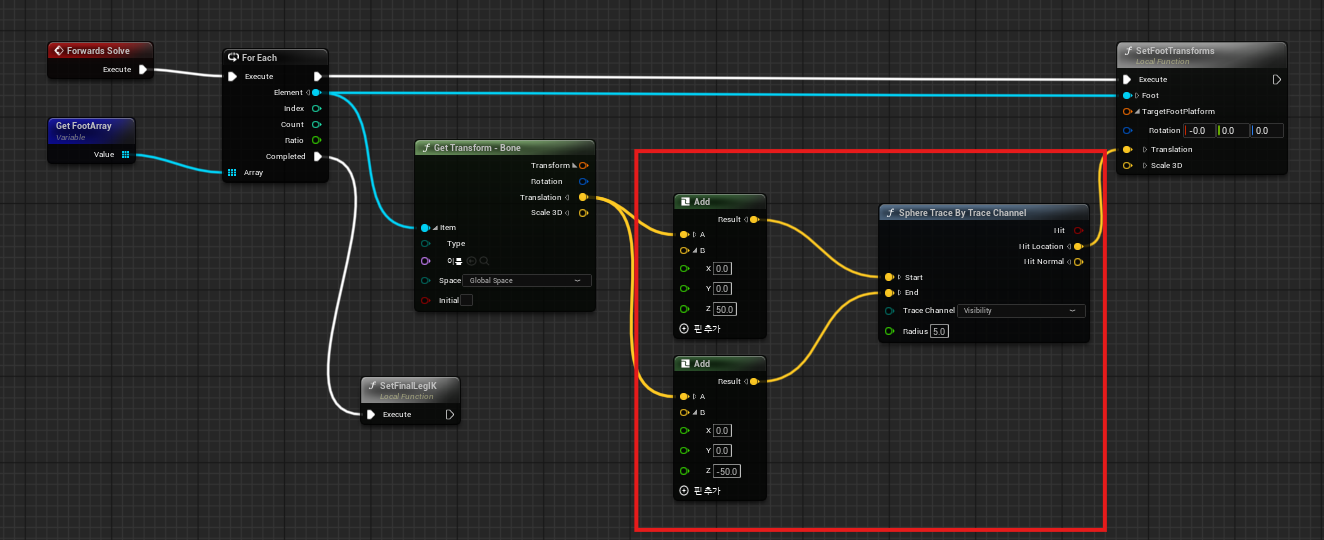
캐릭터가 걷기 위해서는 발이 딛을 땅이 어디에 있는지 알아야 한다.

For Each루프를 돌며 각 발의 위치에서 바닥을 향해 레이(Ray)를 쏜다.

  • 저장해 둔 FootArray를 활용한다.
  • Sphere Trace By Trace Channel을 사용해 발보다 50 높은 위치에서 발보다 50 낮은 방향으로 Sphere Trace를 실행한다.
  • 바닥에 닿으면 그 위치(Hit Location)를 통해 발이 가야 할 목표(TargetFootPlatform)를 결정한다.

image-20260116231223149

3. 발의 위치 및 오프셋 계산 (Foot Transform Logic)

단순히 발을 바닥 포인트에 옮기는 것만으로는 부족하다.

발목(Foot)과 발볼(Ball)의 위치 관계를 고려해 정확한 착지 지점을 계산해야 한다.

이후 계산된 위치로 발을 이동시키고, 경사면에 맞춰 발목을 회전한다.

SetFootTransforms 함수 내부

  • 현재 처리 중인 FootReference과 그 자식인 BallReference를 설정한다.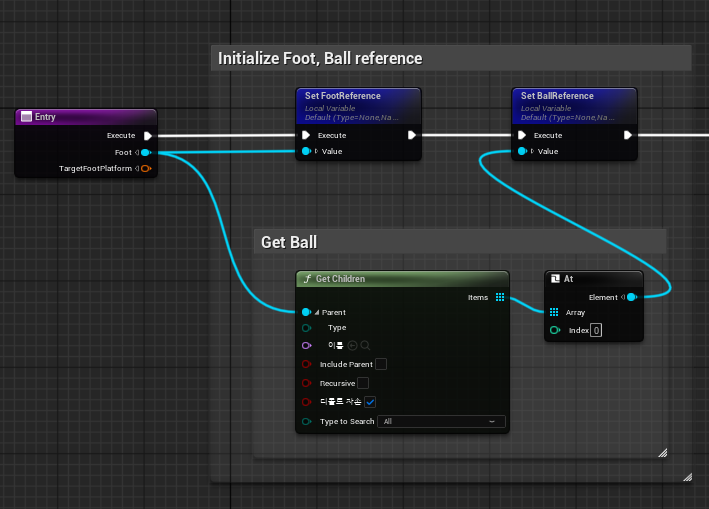 image-20260116231546130

  • Thigh부터 바닥까지의 거리를 계산하고, Dot Product를 사용해 다리의 방향성을 FootFowordOffset에 저장한다.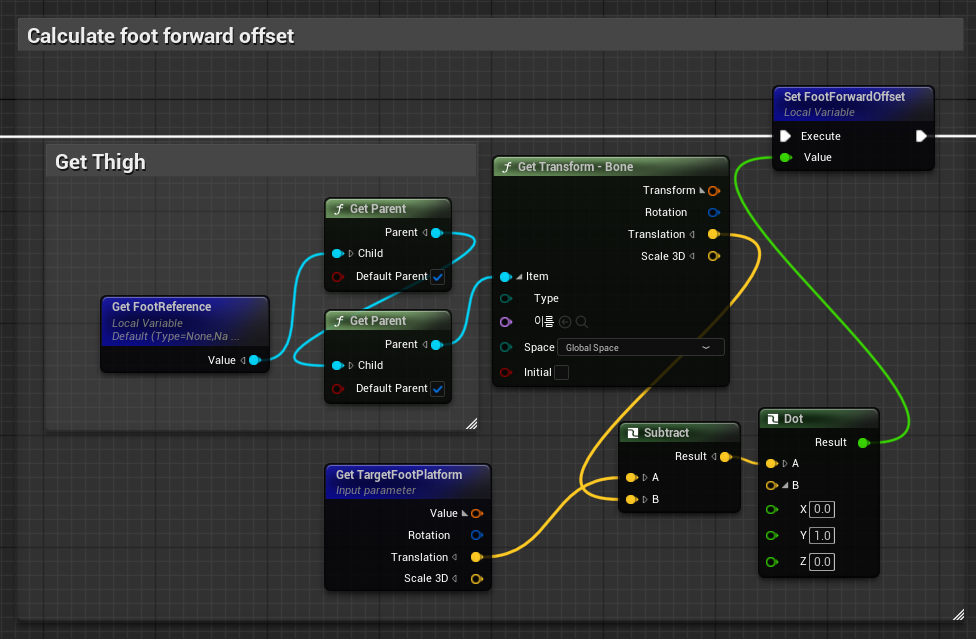 image-20260116231815966

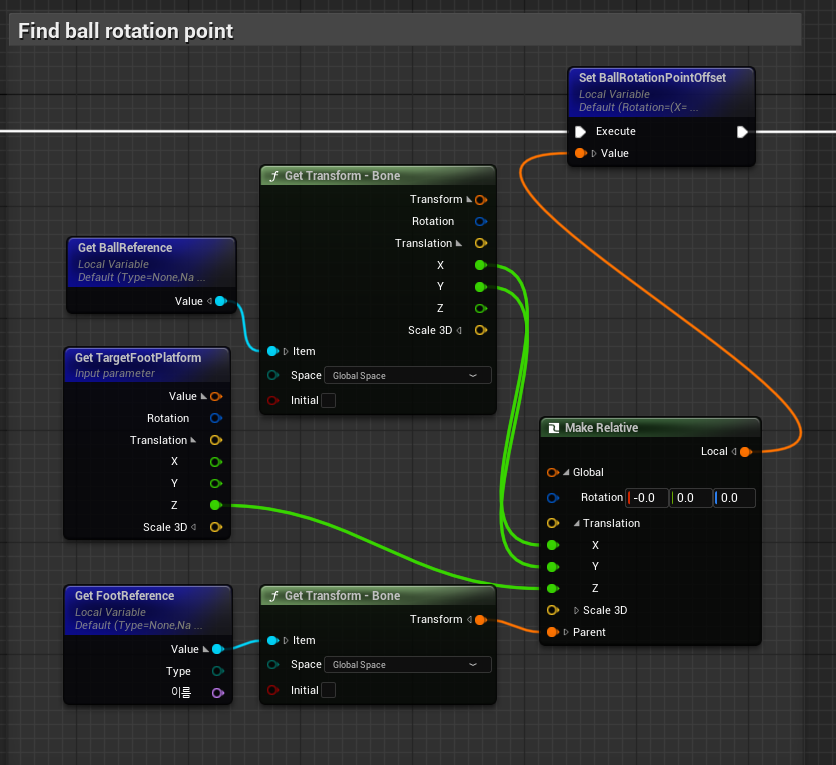
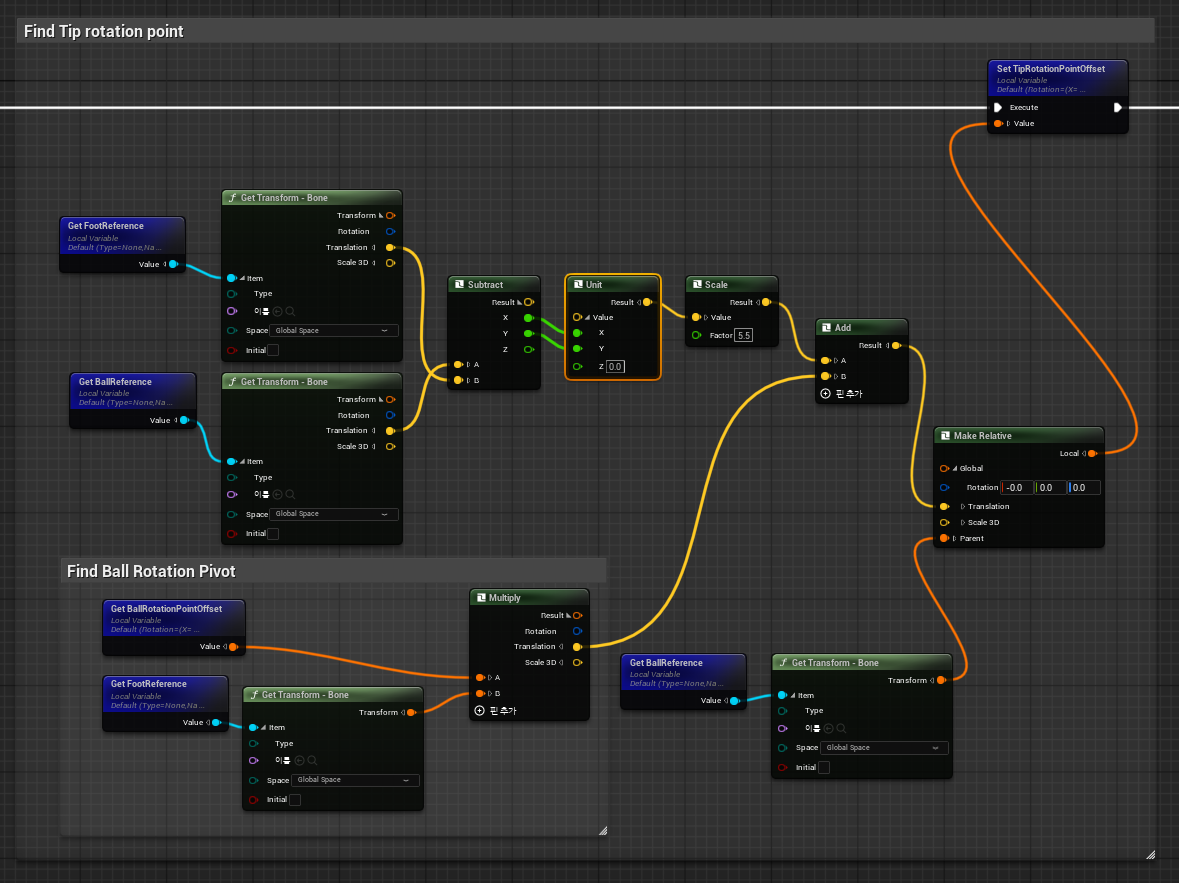
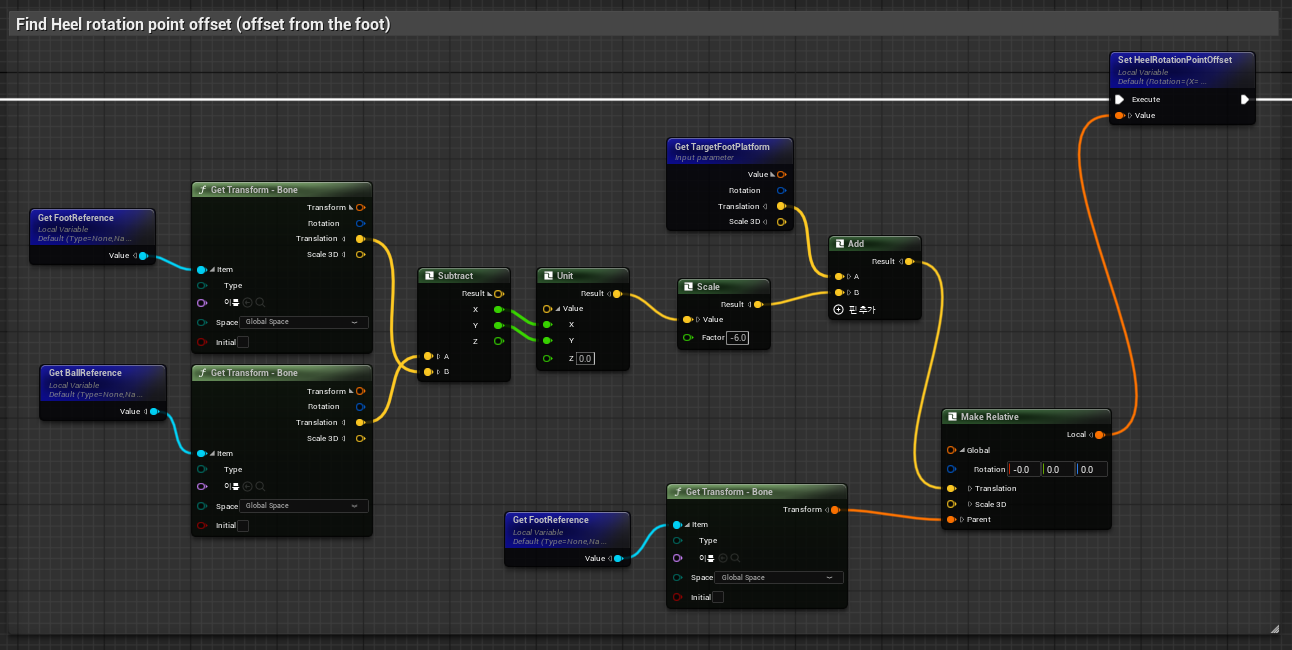
  • Make Relative - 월드 공간의 좌표를 부모 본 기준의 로컬 좌표로 변환해, 캐릭터가 이동해도 더블(?)로 적용 되지 않도록 BallRotationPointOffset, TipRotationPointOffset, HeelRotationPointOffset을 설정한다. image-20260116232357974 image-20260117140006932 image-20260117140106397

  • Set Transform - Bone을 통해 계산된 최종 위치값에 Z축 오프셋(발바닥 두께)을 더해 Foot 본을 실제로 이동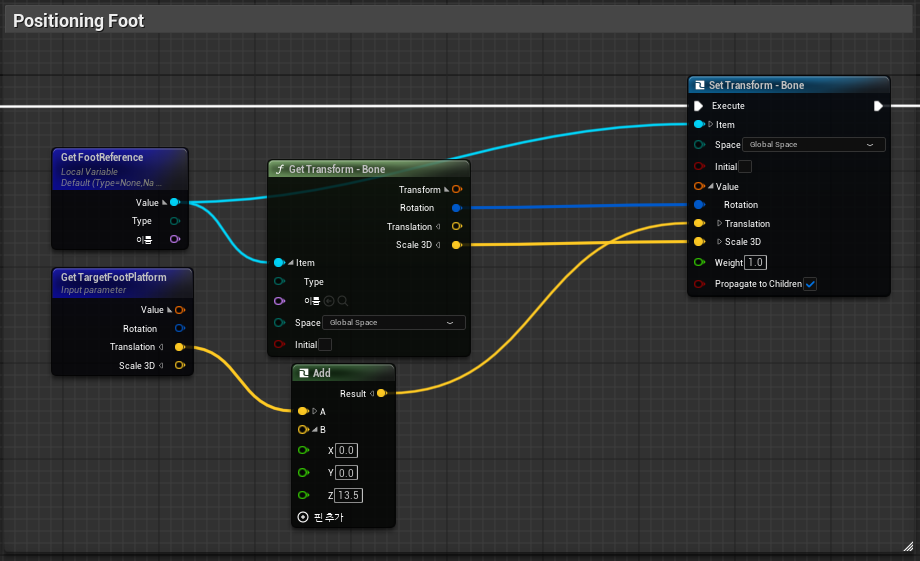 image-20260116232742252

  • RotateAroundPoint는 지형이 기울어져 있을 때 발이 파묻히거나 뜨지 않도록, 접촉면을 기준으로 발을 회전시키는 함수이다.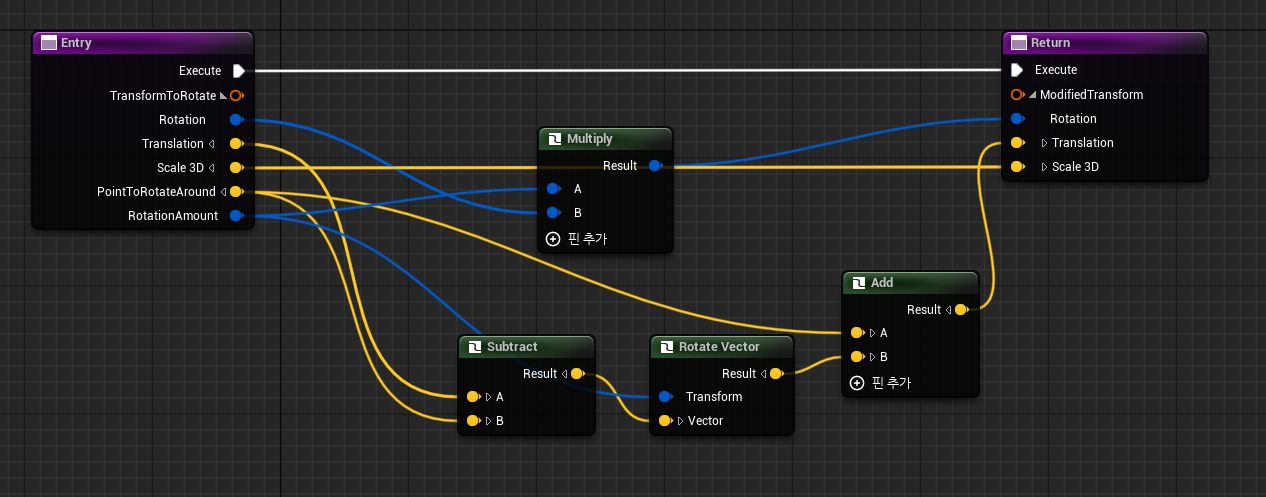 image-20260116234128832

    • 특정 위치를 중심으로 물체를 공전시키듯 회전 하기 위해 작성되었다.

    • 핵심원리는 이동(Translate) -> 회전(Rotate) -> 복귀(Translate Back) \(P' = R \cdot (P - C) + C\)

      • P - 원래 위치
      • C - 회전의 중심점
      • R - 회전할 각도
      • P’ - 최종 위치

    • Subtract: 원점으로 가져오기 \((P - C)\)

      • 노드: Translation (A) - PointToRotateAround (B)

      • 의미: 물체의 위치에서 회전축의 위치를 뺍니다.

      • 수학적 이유:

        • 회전 연산은 기본적으로 (0, 0, 0) 원점을 기준으로 작동.
        • 우리가 원하는 회전축(C)을 임시로 월드의 원점(0, 0, 0)으로 이동시킨다고 상상해 보자.
        • 이렇게 하면 물체의 위치(P)는 “회전축으로부터 떨어진 상대적인 거리와 방향(벡터)”만 남게 된다.
        • 이를 로컬 벡터(Local Vector)화 한다고도 합니다.

    • Rotate Vector: 돌리기 \((R \cdot \text{Vector})\)

      • 노드: Subtract의 결과(벡터)를 RotationAmount만큼 회전

      • 의미: 방금 구한 “회전축에서 물체까지의 벡터”를 원하는 각도만큼 휘전.
      • 수학적 이유:
        • 이제 기준점이 원점이 되었으므로, 단순히 회전 행렬(혹은 쿼터니언)을 곱하면 물체는 회전축 주변을 공전하듯이 이동하게 된된다.

    • Add: 원래 자리로 되돌리기 \((+ C)\)

      • 노드: Rotate Vector의 결과 + PointToRotateAround
      • 의미: 아까 1단계에서 임시로 원점으로 가져왔던 세계를 다시 원래 위치로 되돌려 놓는다.
      • 수학적 이유:
        • 회전이 끝난 벡터에 다시 회전축의 원래 위치(C)를 더해줌으로써, 월드 공간(Global Space)에서의 올바른 최종 위치를 확정 짓는다.

    • Multiply: 회전값 곱하기

      • 노드: Rotation * RotationAmount

      • 이유:

        • 위의 단계는 물체의 위치(Position/Translation)만 바꾼 것이다 (공전).

        • 물체가 궤도를 돌 때 물체 자체도 회전(자전)해야 자연스럽다.

        • 발이 경사면을 따라 위치가 바뀌었다면 발바닥의 각도도 그 경사면에 맞춰 꺾여야 한다. 그래서 기존 회전값에 추가 회전값을 곱해서 방향(Orientation)도 함께 업데이트해 주는 것.

댓글남기기

참고